Speculative Decoding with Blockwise Sparse Attention
Speculative decoding (SD) and blockwise sparse attention both accelerate LLM decoding, but when combined naively, the KV cache may lose sparsity during the verification step of SD. We show that forcing all draft tokens to attend to the same subset of the context restores sparsity while preserving model quality.
Introduction
Scaling the context length of LLMs continues to be crucial for improving their capabilities and unlocking new categories of applications. However, this leaves a greater proportion of newer ML accelerators underutilized, since it decreases the operational intensity of generating tokens.
New attention mechanisms such as DeepSeek’s Native Sparse Attention (NSA) and Moonshot AI’s Mixture of Block Attention (MoBA) divide the context into blocks and allow each token to dynamically attend to just a subset of these blocks. By reducing the volume of data that needs to be moved from high bandwidth memory (HBM) into compute cores, these “blockwise sparse” methods aim to increase the operational intensity of decoding.
Speculative decoding (SD) similarly increases the operational intensity of decoding, and has been widely implemented to reduce latency or increase throughput by around 2×. Unfortunately, naively combining blockwise sparsity with SD by using a blockwise sparse target model falls short of its potential: when each draft token loads a different set of blocks from HBM, the operational intensity of verification drops significantly.
In this article, we train NSA models in which a block of tokens attend to the same subset of the context in the “token selection” attention path. We show that these models have the same language modeling quality as baseline NSA models, while achieving up to 3.5× higher operational intensity during the verification step of speculative decoding.
Our implementation of NSA, a supporting notebook, and code used to produce figures are available at https://github.com/MatX-inc/seqax/tree/NSA.
Verification may be much slower with a blockwise sparse target model
Speculative decoding uses a cheap draft model to generate candidate tokens that are verified in parallel by a target model. SD reduces the latency or increases the throughput of decoding by the factor where a round of speculation is the generation and subsequent verification of each block of draft tokens, and are the latencies of a draft and target model forward pass on a single token, and is the latency of a target model forward pass on tokens.
If and we can change without changing , , or , the speedup is inversely proportional to . Since verification with a long context has low operational intensity, is directly proportional to the number of context tokens that must be loaded. Thus, reducing by some factor increases the speedup due to SD by the same factor.
| Context Length | 8192 | 16384 | 32768 | 65536 |
|---|---|---|---|---|
| Full Attention | 8192 | 16384 | 32768 | 65536 |
| NSA (verification best case) | 2048 | 2560 | 3584 | 5632 |
| NSA (verification worst case) | 5120 | 5632 | 6656 | 8704 |
| NSA (reduction in memory access volume in best case compared to worst case) | 2.5× | 2.2× | 1.9× | 1.5× |
Table 1: Memory access volume (in equivalent number of tokens) during a forward pass (the size of the KV cache is the same when decoding one token or verifying draft tokens. Here, ). Adapted from Yuan et al.’s Table 4.
Table 1 shows the difference in in the best and worst cases when . In the best case, each draft token attends to the same subset of the context, and in the worst case, each draft token attends to a different subset of the context. In the limit as the batch size tends to infinity (or equivalently, assuming that the latency of loading the model’s parameters from HBM is negligible), Figure 1 shows that the operational intensity of verification (and therefore the speedup due to SD) may be over 3.5× higher in the best case than in the worst case.
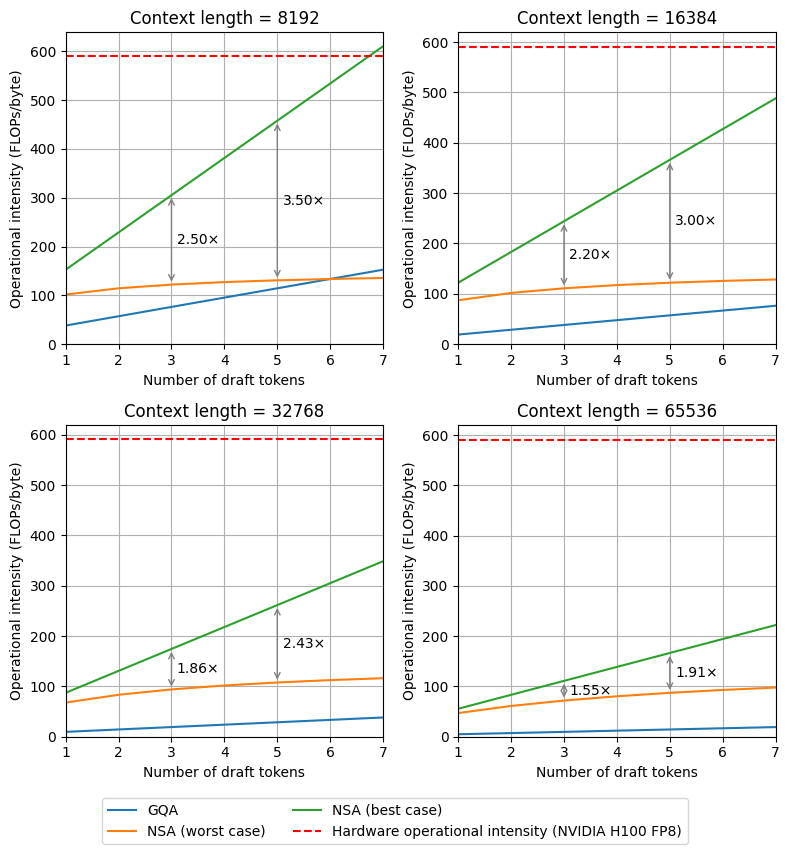
Figure 1: Operational intensity of verification as a function of the number of draft tokens for target models with 3B active parameters, 30 layers, 4 GQA groups, key dimension , and value dimension . In the best case, each draft token selects the same subset of the context, and in the worst case, each draft token selects a different subset of the context.
We can force a block of tokens to attend to the same subset of the context
To always achieve the best case operational intensity during verification, we replace with , where are the keys and values selected by token . During training, for each which is a multiple of , is reused by the tokens following token . During each verification forward pass, the query sequence length is equal to , so the keys and values selected by the first token are attended to by all subsequent tokens.
We simulate loading only selected keys and values from HBM using the attention mask shown in Figure 2 (left). Forcing a block of query tokens to attend to the same subset of the context corresponds to using an attention mask like the one shown in Figure 2 (right). Figure 3 zooms in on the last rows of each mask (here, ) and shows that in this instance, our modification lets us load fewer KV blocks during verification.
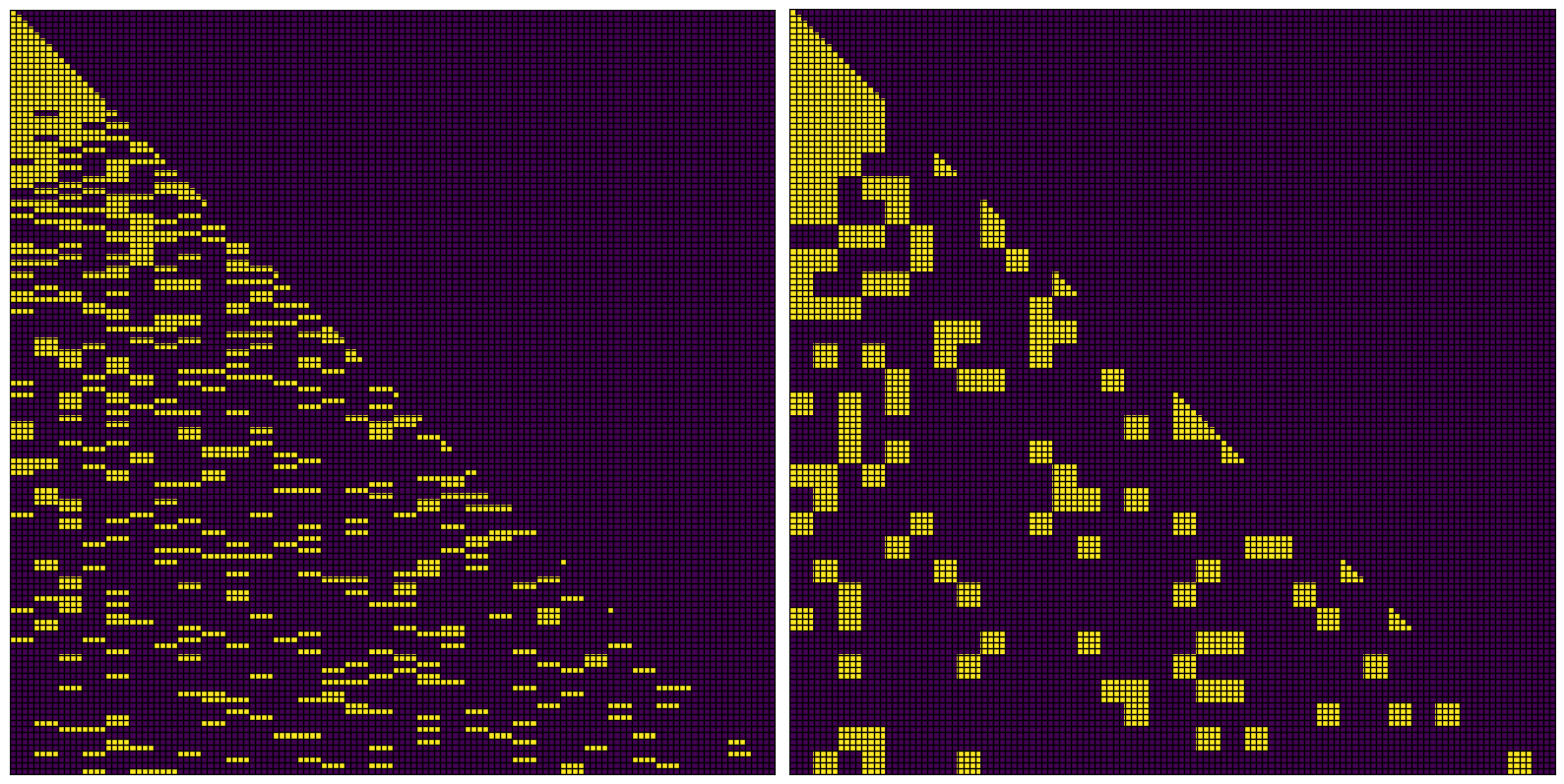
Figure 2: Left is a selected attention mask constructed using uniformly random importance scores . Right is the attention mask obtained by applying our modification to left, which forces blocks of tokens (here, ) to select the same subset of the context. As in the selected attention mask in Yuan et al.’s Figure 2, yellow squares indicate which attention scores must be computed.

Figure 3: Above are the last four rows of Figure 2 (left) and below are the last four rows of Figure 2 (right). Both are examples of a selected attention mask when performing a forward pass on tokens in parallel (here, ).
Table 2 shows that for models with 184 million and 1.2 billion parameters, the cross-entropy on a slice of the LongCrawl64 validation set is approximately equal for different numbers of draft tokens . We train all models on 10B tokens from a slice of the LongCrawl64 training set, with a sequence length of 2048. The attention sublayer in each model is our best interpretation of NSA presented by Yuan et al., and we use , , , , and . The feed-forward sublayer in each model is a dense (SwiGLU) layer rather than a Mixture of Experts (MoE) layer, and we use multiple RMSNorms in each sublayer. All models are trained for 19070 steps using the AdamW optimizer with a batch size of 256, , and with a weight_decay of . Over the first 1907 steps we linearly increase the learning rate from 0 to one of the learning rates in (using a smaller peak learning rate for larger models), before decaying it to 1% of the peak learning rate following a cosine decay schedule.
| Parameters | NSA | |||
|---|---|---|---|---|
| 186M | 2.128 | 2.128 | 2.128 | 2.13 |
| 1177M | 1.794 | 1.794 | 1.793 | 1.794 |
Table 2: Cross-entropy on a slice of the LongCrawl64 validation set is approximately equal across different numbers of draft tokens for models with 184 million and 1.2 billion parameters.
Figure 4 shows that training loss curves for models with 1.2 billion parameters are essentially identical.
Figure 4: (Interactive) loss curves show that forcing blocks of tokens to attend to the same subset of the context maintains model quality for .
Ablations
Yuan et al. always select the first and last two blocks in the token selection attention path. Since our training sequence length is 2048 rather than Yuan et al.’s 8192, we select a total of rather than blocks. However, these choices together may limit the maximum possible effect size of our modification, since the single dynamically-selected block may barely affect model quality.
Thus, we try a) training models which do not always select the first and last two blocks. We also try b) training a model without token selection, to rule out the possibility that this entire attention path barely affects model quality, and we try a training-free method c) which applies our modification at test-time.
| Summary | Description | NSA | ||||
|---|---|---|---|---|---|---|
| 1 | b) | (no selection) | 2.147 | |||
| 2 | Baseline () | 2.128 | 2.128 | 2.128 | 2.130 | |
| 3 | a) | Freely select blocks | 2.132 | 2.129 | 2.126 | 2.127 |
| 4 | c) | at test-time | 2.128 | 2.129 | 2.132 | 2.134 |
| 5 | a), c) | Freely select at test-time | 2.132 | 2.132 | 2.133 | 2.135 |
Table 3: Cross-entropy on a slice of the LongCrawl64 validation set for models with 184 million parameters.
Table 3 shows that with ablation a), model quality varies more but does not degrade as increases from 0 to 7. With the other two ablations, model quality degrades slightly but monotonically as increases from 0 to 7; comparing row 2 with 4 and row 3 with 5 indicates train-test mismatch. While the gap between no selection and the baseline () is only 0.019, this difference is still meaningful: factors such as GPU non-determinism, initialization seed, and data ordering led to variations in cross-entropy of just a couple of thousandths.
We also tried d) selecting a total of blocks, and observed that model quality is preserved with any combination of a) and d). Indeed, although token selection has a greater effect on model quality as increases, for large enough the maximum possible effect size of our modification is smaller than when , since there is greater overlap between the subsets of the context attended to by each token.
Discussion
Yuan et al. say that their Figure 8 (visualization of attention map) inspired their design of NSA since they observed “nearby keys often showing similar attention scores”. We further suggest that this figure shows many different queries attending to the same keys, and is an alternative motivation for forcing a block of tokens to attend to the same subset of the context.
Limitations of our results are that we evaluated small models with short contexts from a single dataset, and that cross-entropy alone is insufficient for evaluating long-context performance. Our implementation of NSA uses dense (SwiGLU) layers rather than Mixture of Experts (MoE) layers to mix information along the model dimension, and there may be an interaction between blockwise sparse attention and the type of mixer used.
We have shown that we can force a block of tokens to attend to the same subset of the context while preserving model quality. Our ablations rule out the possibility that selected attention does not affect model quality with our hyperparameters, and show that training with our modification reduces train-test mismatch (but may not be necessary when the number of draft tokens is small).
